
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Примеры решения задач
ЗАДАЧА 1. Радиус-вектор точки А относительно начала координат меняется со временем по закону  , где a и b – постоянные, a (м/с), b (м/с2);
, где a и b – постоянные, a (м/с), b (м/с2); 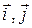 – орты осей X и Y. Найти: а) уравнение траектории точки, изобразить ее график; б) зависимость от времени угла j между векторами
– орты осей X и Y. Найти: а) уравнение траектории точки, изобразить ее график; б) зависимость от времени угла j между векторами  и
и 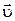 .
.
ДАНО:
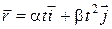
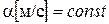 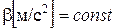
|
 –? –?  –? –?
|
АНАЛИЗ. Предлагаемая задача – обратная задача кинематики. По известному закону движения в векторной форме требуется определить уравнение траектории. Для этого необходимо записать закон движения в координатной форме и исключить время в полученной системе уравнений. Чтобы установить зависимость скорости материальной точки от времени, целесообразно найти проекции вектора скорости на координатные оси, продифференцировав соответствующие уравнения движения, а затем дать векторную запись 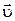 . Вектор ускорения найдем, взяв производную от вектора скорости.
. Вектор ускорения найдем, взяв производную от вектора скорости.
Для определения угла между векторами  и
и  следует воспользоваться их скалярным произведением. Однако можно поступить проще, если вектор ускорения направлен по одной из координатных осей. В этом случае искомый угол – это угол между вектором скорости и соответствующей осью.
следует воспользоваться их скалярным произведением. Однако можно поступить проще, если вектор ускорения направлен по одной из координатных осей. В этом случае искомый угол – это угол между вектором скорости и соответствующей осью.
 Рис. 1.1.5
Рис. 1.1.5
|
РЕШЕНИЕ. По заданному в условии задачи закону движения напишем компоненты радиус-вектора:
x (t) = a t; y (t) = b t 2; z (t) = 0. (1.1.1)
Из этих выражений видно, что движение материальной точки происходит в плоскости 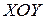 , из первого уравнения выражаем
, из первого уравнения выражаем 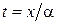 и подставляем его во второе: y = b x 2/a2– это искомое уравнение траектории. Точка движется по параболе, график которой представлен на рис. 1.1.5.
и подставляем его во второе: y = b x 2/a2– это искомое уравнение траектории. Точка движется по параболе, график которой представлен на рис. 1.1.5.
Проверим размерность:  = м.
= м.
Дифференцируя систему уравнений (1.1.1), находим компоненты вектора скорости:
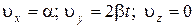 и
и 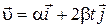 , его модуль
, его модуль  .
.
Вектор ускорения равен 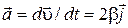 – частица движется с постоянным ускорением, направленным по оси Y, модуль которого
– частица движется с постоянным ускорением, направленным по оси Y, модуль которого  .
.
Найдем угол j между векторами  и
и 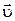 . Из рис. 1.1.5 видно, что это угол между вектором скорости
. Из рис. 1.1.5 видно, что это угол между вектором скорости 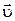 и осью Y, следовательно,
и осью Y, следовательно, 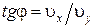 , подставив значения
, подставив значения  и
и 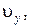 получаем: tgj = a/(2b t).
получаем: tgj = a/(2b t).
Правильность формулы по размерности очевидна.
ОТВЕТ: y = b x 2 / a2, tgj = a/(2b t).
ДАНО:
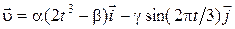 a = 1 м/с4; b = 1 c3; g = 1 м/c
t = 0; a = 1 м/с4; b = 1 c3; g = 1 м/c
t = 0; 
|
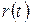 –? –?
|
ЗАДАЧА 2. Скорость материальной точки изменяется по закону  , где a = 1 м/с4, b = 1 c3, g = 1 м/c. Определить закон движения, если в начальный момент времени (t = 0) точка находилась в начале координат
, где a = 1 м/с4, b = 1 c3, g = 1 м/c. Определить закон движения, если в начальный момент времени (t = 0) точка находилась в начале координат 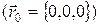 .
.
АНАЛИЗ. В задаче дан закон изменения вектора скорости со временем. Для определения закона движения следует проинтегрировать его по времени с учетом начальных условий.
РЕШЕНИЕ: Согласно условию задачи,
компоненты вектора скорости известны:
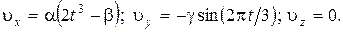 (1.1.2)
(1.1.2)
Интегрируя выражения (1.1.2), получаем уравнение движения в проекциях на координатные оси:

Окончательно: 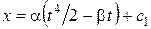 ;
; 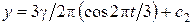 ;
;  , (1.1.3)
, (1.1.3)
где с 1, с 2, и с 3– постоянные, которые определяются из начальных условий; учитывая, что x = 0, y = 0, z = 0 при t = 0, получаем c1 = 0; c 2 = –3g/(2p); c 3 = 0.
Тогда (1.1.3) перепишем следующим образом:
 ;
; 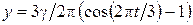 ;
; 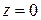
х = a(0,5 t 4 – b t); y = 3g/2p(cos(2p t /3) – 1); z = 0.
Искомое уравнение движения материальной точки имеет вид:
 .
.
Проверим размерность  .
.
ОТВЕТ:  .
.
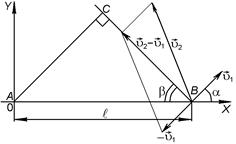
ЗАДАЧА 3. Из двух портов А и В, расстояние между которыми равно 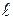 , одновременно выходят два катера, один из которых плывет со скоростью
, одновременно выходят два катера, один из которых плывет со скоростью 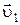 , а другой – со скоростью
, а другой – со скоростью 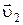 (рис 1.1.6). Направление движения первого катера составляет угол a, а второго – угол b с линией АВ. Каким будет наименьшее расстояние между катерами?
(рис 1.1.6). Направление движения первого катера составляет угол a, а второго – угол b с линией АВ. Каким будет наименьшее расстояние между катерами?
ДАНО:
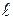 (м); (м); 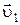 (м/с); (м/с); 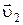 (м/с)
a(рад); b (рад) (м/с)
a(рад); b (рад)
|
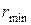 –? –?
|
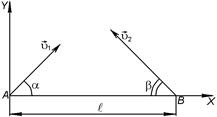 АНАЛИЗ. Эта задача на кинематику совместного движения тел. В условии задачи даны скорости тел и направления движения. Требуется определить наименьшее расстояние между телами. Решение задачи можно осуществлять либо в системе отсчета, связанной с Землей, либо с одним из тел. В последнем случае для определения относительной скорости следует воспользоваться теоремой сложения скоростей.
АНАЛИЗ. Эта задача на кинематику совместного движения тел. В условии задачи даны скорости тел и направления движения. Требуется определить наименьшее расстояние между телами. Решение задачи можно осуществлять либо в системе отсчета, связанной с Землей, либо с одним из тел. В последнем случае для определения относительной скорости следует воспользоваться теоремой сложения скоростей.
РЕШЕНИЕ. 1способ. Оба тела движутся прямолинейно и равномерно. Поскольку размеры тел много меньше рассматриваемых расстояний, тела будем считать материальными точками. За начало отсчета примем точку А. Законы движения известны, поэтому радиус-векторы тел в любой момент времени определяются выражениями:
 ,
,
а расстояние между ними r равно 
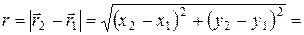
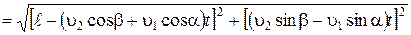 . (1.1.4)
. (1.1.4)
Чтобы определить наименьшее  необходимо найти время
необходимо найти время  , при котором функция (1.1.4) имеет минимум. Для этого следует взять производную функции r по времени и приравнять ее к нулю. Возведя (1.1.4) в квадрат, получаем:
, при котором функция (1.1.4) имеет минимум. Для этого следует взять производную функции r по времени и приравнять ее к нулю. Возведя (1.1.4) в квадрат, получаем: 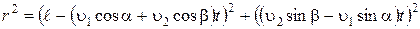 .
.
Найдем производную от обеих частей последнего выражения:

Выразим  и приравняем его к нулю:
и приравняем его к нулю:  = 0, тогда момент времени t min, в который расстояние между катерами минимально, равен:
= 0, тогда момент времени t min, в который расстояние между катерами минимально, равен:
 . (1.1.5)
. (1.1.5)
Подставив (1.1.5) в формулу (1.1.4), находим минимальное расстояние между катерами:
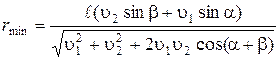 . (1.1.6)
. (1.1.6)
Проверим размерность:  .
.
2 способ. Свяжем инерциальную систему отсчета с первым катером. Второй катер относительно этой системы отсчета движется со скоростью  а траекторией его является прямая ВС (рис. 1.1.7). Очевидно, что минимальное расстояние между катерами есть длина перпендикуляра АС, опущенного из точки А на прямую ВС:
а траекторией его является прямая ВС (рис. 1.1.7). Очевидно, что минимальное расстояние между катерами есть длина перпендикуляра АС, опущенного из точки А на прямую ВС: 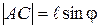 ,где j – угол между направлением ВА и вектором
,где j – угол между направлением ВА и вектором 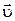 .
.
Для нахождения sinj спроектируем 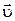 на ось OY, получаем:
на ось OY, получаем: 
По теореме косинусов 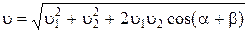 ,
,
отсюда  .
.
Окончательно имеем:  ,
,
что совпадает с решением (1.1.6), полученным первым способом.
ОТВЕТ:  .
.
ЗАДАЧА 4. Из пункта А на берегу канала с неподвижной водой надо попасть в пункт В на противоположном берегу. Все расстояния показаны на рис.1.1.8. Человек плывет через канал на лодке со скоростью  , а дальше идет пешком со скоростью
, а дальше идет пешком со скоростью 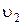 . Доказать, что из А в В быстрее всего он попадет, если углы a1 и a2 удовлетворяют условию:
. Доказать, что из А в В быстрее всего он попадет, если углы a1 и a2 удовлетворяют условию: 
ДАНО:
 ; ; 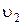
|
ДОКАЗАТЬ: 
|
 АНАЛИЗ. Тело последовательно участвует в двух прямолинейных равномерных движениях – по воде канала со скоростью
АНАЛИЗ. Тело последовательно участвует в двух прямолинейных равномерных движениях – по воде канала со скоростью 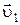 вдоль прямой АС, и по берегу со скоростью
вдоль прямой АС, и по берегу со скоростью 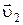 вдоль прямой СВ. В зависимости от положения точки С на рис. 1.1.8 пройденный телом путь, а следовательно, и время движения, будут различны. Положение точки С определяет соотношение между углами
вдоль прямой СВ. В зависимости от положения точки С на рис. 1.1.8 пройденный телом путь, а следовательно, и время движения, будут различны. Положение точки С определяет соотношение между углами 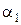 и
и 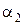 на рисунке.
на рисунке.
РЕШЕНИЕ. Направим ось Х по границе раздела «канал-суша», за начало отсчета примем координату точки А. Расстояние ОС обозначим через х. Тогда путь, который человек проплыл на лодке, равен  =
= 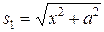 и пройден за время
и пройден за время 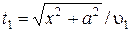 . Путь, пройденный пешком, равен
. Путь, пройденный пешком, равен 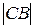 =
=  , время движения по этому пути
, время движения по этому пути 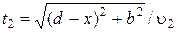 .
.
Полное время движения 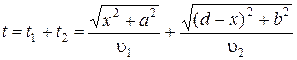
является функцией только координаты х, определяющей положение точки С. Чтобы найти минимум t, необходимо взять производную от функции t (x) по х и приравнять ее к нулю: dt / dx = 0.
Имеем  . (1.1.7)
. (1.1.7)
Из рис. 1.1.5 видно, что 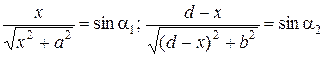 .
.
Тогда выражение (1.1.7) можно представить в виде: 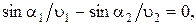
откуда 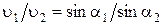 . Правильность формулы по размерности очевидна.
. Правильность формулы по размерности очевидна.
ОТВЕТ: 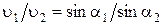 .
.
ЗАДАЧА 5. Лодочник должен переплыть реку из пункта А в пункт В, лежащие на одном перпендикуляре. Если лодочник направляет лодку по прямой АВ (рис. 1.1.9 а), то через время t 1 = 10 мин он попадает в пункт С, лежащий на расстоянии s = 120 м по течению ниже, чем пункт В. Если он направит лодку под некоторым углом к прямой АВ (рис. 1.1.9 б), то через время t 2= 12,5 мин попадет в пункт В. Считая скорость лодки относительно воды постоянной, определить скорость  течения реки, относительную скорость
течения реки, относительную скорость 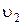 лодки, ширину реки
лодки, ширину реки 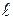 и угол a между вектором скорости лодки и прямой АВ.
и угол a между вектором скорости лодки и прямой АВ.
| ДАНО: t 1 = 600 с s = 120 м t 2= 720 с |
 –? –? 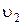 –? –? 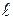 –?
a –? –?
a –?
|
АНАЛИЗ. Лодка с гребцом участвует в двух движениях:
1) движение лодки вместе с рекой происходит параллельно берегам с постоянной скоростью 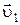 ;
;
2) движение лодки относительно воды с постоянной скоростью 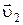 возникает под действием усилий гребца.
возникает под действием усилий гребца.
Векторная сумма этих скоростей есть результирующая скорость лодки относительно берега. В первом случае она направлена по прямой АС, во втором – по прямой АВ.
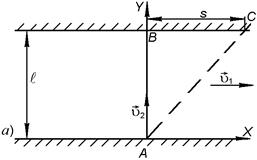
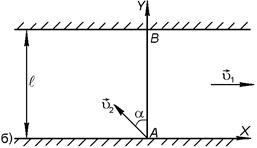 Рис. 1.1.9
Рис. 1.1.9
|
Выберем координатные оси следующим образом. Ось Х направим по течению реки, ось Y – перпендикулярно течению (по направлению АВ). За начало отсчета примем точку А.
РЕШЕНИЕ. В первом случае уравнения движения лодки в проекциях на координатные оси имеют вид:
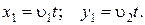 (1.1.8)
(1.1.8)
В момент времени t = t 1 лодка попала в пункт С, при этом  , а выражения (1.1.8) перепишем так:
, а выражения (1.1.8) перепишем так:
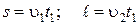 . (1.1.9)
. (1.1.9)
Для второго случая вектор скорости 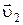 лодки разложим на составляющие по координатным осям:
лодки разложим на составляющие по координатным осям:
 .
.
Тогда результирующая скорость лодки по оси X равна  по оси Y она оказывается равной
по оси Y она оказывается равной  и уравнения движения принимают вид:
и уравнения движения принимают вид:

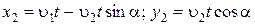 . (1.1.10)
. (1.1.10)
В момент времени  лодка попадает в пункт В, при этом
лодка попадает в пункт В, при этом 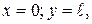 и из уравнений (1.1.10) имеем:
и из уравнений (1.1.10) имеем:
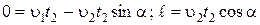 . (1.1.11)
. (1.1.11)
Из выражений (1.1.9) находим скорость течения реки 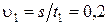 м/с.
м/с.
Решая совместно уравнения (1.1.9) и (1.1.11), находим угол между вектором скорости и прямой АВ:
cosa = t 1/ t 2 = 0,8;a = arcco s 0,8» 37°.
Отсюда 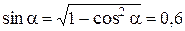 ;
;
скорость лодки относительно воды равна 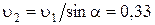 м/с,
м/с,
а ширина реки  м.
м.
Правильность формул по размерности очевидна.
ОТВЕТ:  м/с;
м/с; 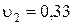 м/с;
м/с; 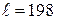 м; a = 37°.
м; a = 37°.
ЗАДАЧА 6. Поезд движется прямолинейно со скоростью  = 180 км/ч. Внезапно на пути возникает препятствие, и машинист включает тормозной механизм. С этого момента скорость поезда уменьшается по закону
= 180 км/ч. Внезапно на пути возникает препятствие, и машинист включает тормозной механизм. С этого момента скорость поезда уменьшается по закону 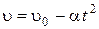 , где
, где 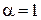 м/с3. Каков тормозной путь поезда? Через какое время после начала торможения он остановится?
м/с3. Каков тормозной путь поезда? Через какое время после начала торможения он остановится?
ДАНО:
 =50 м/с =50 м/с
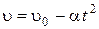
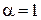 м/с3 м/с3
|
| x –? t–? |
АНАЛИЗ. Эта задача на кинематику прямолинейного замедленного движения. Из закона изменения скорости видно, что скорость пропорциональна квадрату времени, следовательно, ускорение не является постоянным.
Чтобы найти время торможения t, т. е. время после начала торможения, через которое тело остановится, необходимо скорость приравнять к нулю. В процессе движения направление скорости не меняется, а ее значение убывает от  до нуля, т. е. в течение всего времени торможения скорость остается неотрицательной. Поэтому модуль скорости равен ее проекции на направление движения в любой момент времени
до нуля, т. е. в течение всего времени торможения скорость остается неотрицательной. Поэтому модуль скорости равен ее проекции на направление движения в любой момент времени 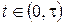 . В этом случае пройденный за время tпуть (тормозной путь) равен интегралу от функции скорости по времени с пределами интегрирования от 0 до t.
. В этом случае пройденный за время tпуть (тормозной путь) равен интегралу от функции скорости по времени с пределами интегрирования от 0 до t.
 Рис. 1.1.10
Рис. 1.1.10
|
РЕШЕНИЕ. Ось X направим по движению поезда. Путь, пройденный поездом до остановки, найдем из выражения:
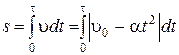 . (1.1.12)
. (1.1.12)
Поскольку за время tскорость тела не меняет направления, модуль в выражении (1.1.12) можно опустить, тогда
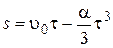 . (1.1.13)
. (1.1.13)
Скорость точки в момент остановки (при t = t) равна нулю:  ,
,
отсюда  .
.
Проверим размерность:  , подставив значения, получаем
, подставив значения, получаем 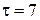 с.
с.
Подставляя  в выражение (1.1.13), получаем:
в выражение (1.1.13), получаем:
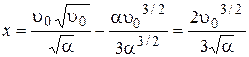 .
.
Проверим размерность: 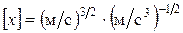
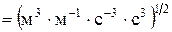 =
=
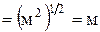 , подставив значения, получим:
, подставив значения, получим: 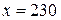 м.
м.
ОТВЕТ: 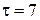 с;
с; 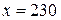 м.
м.
ЗАДАЧА 7. Ракета стартует с Земли вертикально вверх с ускорением 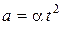 , где a = 1 м/с4. На высоте h = 1000 км двигатели ракеты выходят из строя. Через сколько времени (считая с момента выхода двигателей из строя) ракета упадет на Землю? Сопротивление воздуха не учитывать. Начальная скорость ракеты равна нулю.
, где a = 1 м/с4. На высоте h = 1000 км двигатели ракеты выходят из строя. Через сколько времени (считая с момента выхода двигателей из строя) ракета упадет на Землю? Сопротивление воздуха не учитывать. Начальная скорость ракеты равна нулю.
ДАНО:
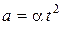 a = 1 м/с4
h = 106 м
a = 1 м/с4
h = 106 м

|
 –? –?
|
АНАЛИЗ. Ракета последовательно участвует в двух прямолинейных движениях. Сначала она движется ускоренно, ускорение растет по величине пропорционально квадрату времени, поэтому движение нельзя считать равноускоренным. В этом движении тело (ракета) проходит расстояние 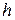 и достигает скорости
и достигает скорости  за время
за время  . Затем двигатели отключаются, и ракета продолжает двигаться по инерции до тех пор, пока ее скорость не уменьшится до нуля за время
. Затем двигатели отключаются, и ракета продолжает двигаться по инерции до тех пор, пока ее скорость не уменьшится до нуля за время 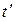 . В этом случае на ракету действует только сила тяжести (сопротивления воздуха нет), и ее ускорение
. В этом случае на ракету действует только сила тяжести (сопротивления воздуха нет), и ее ускорение  . Движение равнозамедленное. За время
. Движение равнозамедленное. За время 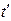 ракета поднимается на высоту
ракета поднимается на высоту 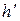 . Полная высота подъема равна
. Полная высота подъема равна 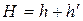 .
.
При решении задачи большое значение имеет абсолютное значение скорости ракеты  в момент отключения двигателей. Ракета движется в поле тяготения Земли, поэтому при
в момент отключения двигателей. Ракета движется в поле тяготения Земли, поэтому при 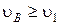 (где
(где 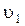 – первая космическая скорость) ракета становится спутником Земли и движется по круговой орбите, при
– первая космическая скорость) ракета становится спутником Земли и движется по круговой орбите, при 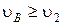 (где
(где  – вторая космическая скорость) ракета покидает орбиту и на Землю не возвращается.
– вторая космическая скорость) ракета покидает орбиту и на Землю не возвращается.
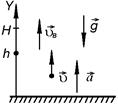 Рис. 1.1.11
Рис. 1.1.11
|
РЕШЕНИЕ. Будем считать ракету материальной точкой. Движение ракеты одномерное. За начало отсчета примем поверхность Земли, ось Y направим вертикально вверх (рис.1.1.11). В начальный момент времени 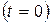 положение ракеты определялось координатой
положение ракеты определялось координатой  . Вспоминая, что ускорение есть производная скорости по времени
. Вспоминая, что ускорение есть производная скорости по времени  или для случая прямолинейного движения
или для случая прямолинейного движения  , выразим дифференциал скорости и после подстановки
, выразим дифференциал скорости и после подстановки  и интегрирования, получим:
и интегрирования, получим:
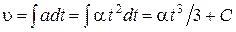 .
.
Константу C находим из начальных условий: в момент времени  скорость
скорость  , поэтому С = 0. Тогда
, поэтому С = 0. Тогда
 . (1.1.14)
. (1.1.14)
Уравнение движения находим после подстановки в 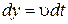 функции u и интегрирования, получим:
функции u и интегрирования, получим: 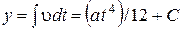 .
.
Подставив начальные условия (у = 0 при t = 0), получаем С = 0 и y = a t 4 / 12.
При y = h двигатели вышли из строя. Это произошло в момент времени
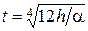 . (1.1.15)
. (1.1.15)
Подставив (1.1.15) в выражение (1.1.14), получаем значение скорости в момент отключения двигателей:  .
.
Проверим размерность:  , подставив значение, имеем:
, подставив значение, имеем: 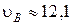 км/с.
км/с.
Это значение превосходит вторую космическую скорость  11,2 км/c, поэтому ракета вообще не возвратится на Землю.
11,2 км/c, поэтому ракета вообще не возвратится на Землю.
ОТВЕТ: Ракета не возвратится на Землю.
ЗАДАЧА 8. Два тела движутся по прямой с ускорениями 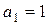 м/с2 и
м/с2 и  м/с2. Некоторую точку A пути второе тело проходит спустя t = 14 с после первого тела в том же направлении. В точке А скорость первого тела
м/с2. Некоторую точку A пути второе тело проходит спустя t = 14 с после первого тела в том же направлении. В точке А скорость первого тела 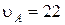 м/с, скорость второго тела
м/с, скорость второго тела 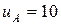 м/с. Через сколько времени после прохождения первым телом точки А оба тела столкнутся?
м/с. Через сколько времени после прохождения первым телом точки А оба тела столкнутся?
ДАНО:
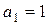 м/с2 м/с2
 м/с2
t = 14 с м/с2
t = 14 с
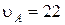 м/с м/с
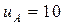 м/с м/с
|
| t –? |
АНАЛИЗ. Задача на кинематику совместного движения двух тел. Чтобы выяснить, когда произойдет столкновение тел, необходимо записать уравнения движения этих тел в выбранной системе отчета. Для описания движения возьмем ось Х, направленную по движению тел. Все характеристики движения (скорости, положения тел) заданы по отношению к точке А,поэтому точку А примем за начало отчета (рис. 1.1.12). Движения обоих тел – равноускоренные с ускорениями  и
и 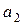 соответственно. В начальный момент времени первое тело находилось в точке А ( в начале отсчета), его скорость в этот момент была равна
соответственно. В начальный момент времени первое тело находилось в точке А ( в начале отсчета), его скорость в этот момент была равна 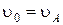 .
.
Второе тело в это время находилось на некотором расстоянии  левее точки А (т. е.
левее точки А (т. е.  ) и имело некоторую скорость
) и имело некоторую скорость 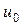 такую, что через
такую, что через  секунд она стала равна
секунд она стала равна  . В этот момент времени второе тело пришло в точку А.
. В этот момент времени второе тело пришло в точку А.
На основании этих данных можно записать уравнения движения тел, и, приравняв их, найти время встречи.
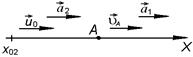 Рис. 1.1.12
Рис. 1.1.12
|
РЕШЕНИЕ. Уравнение движения первого тела
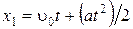 ;
;
второго  ,
,
где  – координата второго тела в момент времени
– координата второго тела в момент времени  ,
, 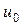 – его начальная скорость.
– его начальная скорость.
По условию задачи  ,
,  . В момент времени
. В момент времени  второе тело находилось левее точки А на оси Х и двигалось к точке А еще
второе тело находилось левее точки А на оси Х и двигалось к точке А еще  секунд. Тогда
секунд. Тогда 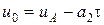 ,
, 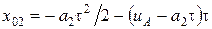 . Окончательно получаем:
. Окончательно получаем: 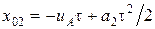 , и уравнение движения второго тела принимает вид:
, и уравнение движения второго тела принимает вид:
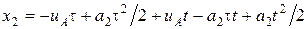 .
.
Время столкновения тел находим из условия 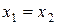 , т. е.
, т. е.
 .
.
Правильность формулы по размерности очевидна.
Решая квадратное уравнение относительно t, получаем два корня: 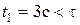 ;
; 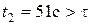 . В первом случае тела движутся навстречу друг другу, и столкновение происходит до того, как оба тела пришли в точку А. Это решение физически не соответствует условию. Во втором случае тела движутся в одном направлении, столкновение происходит после прохождения телами точки А.
. В первом случае тела движутся навстречу друг другу, и столкновение происходит до того, как оба тела пришли в точку А. Это решение физически не соответствует условию. Во втором случае тела движутся в одном направлении, столкновение происходит после прохождения телами точки А.
ОТВЕТ:  .
.
ЗАДАЧА 9. Камень брошен с высоты  м под углом
м под углом 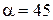 ° к горизонту и падает на Землю на расстоянии
° к горизонту и падает на Землю на расстоянии  м по горизонтали от места бросания. Найти начальную скорость
м по горизонтали от места бросания. Найти начальную скорость  камня, время полета t, максимальную высоту H подъема над уровнем Земли, а также радиусы кривизны траектории в верхней точке и в точке падения камня на Землю.
камня, время полета t, максимальную высоту H подъема над уровнем Земли, а также радиусы кривизны траектории в верхней точке и в точке падения камня на Землю.
ДАНО:
 м м
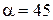 ° °
 м м
|
 ; t; H –? ; t; H –?
 ; ; 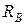 –? –?
|
AНАЛИЗ. Из условия задачи известно направление вектора начальной скорости 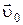 камня, который можно считать материальной точкой. Если пренебречь сопротивлением воздуха, то ускорение камня
камня, который можно считать материальной точкой. Если пренебречь сопротивлением воздуха, то ускорение камня 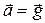 , т. е. постоянно и направлено по вертикали вниз. Векторы начальной скорости и ускорения образуют некоторый угол, не равный ни нулю, ни p.
, т. е. постоянно и направлено по вертикали вниз. Векторы начальной скорости и ускорения образуют некоторый угол, не равный ни нулю, ни p.
Следовательно, движение камня криволинейное. Так как 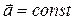 , движение плоское, его можно описать двумя координатами и представить как сумму двух простых движений – равномерного по горизонтали (вектор
, движение плоское, его можно описать двумя координатами и представить как сумму двух простых движений – равномерного по горизонтали (вектор 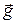 имеет вертикальное направление, и его проекция на горизонтальную ось координат равна нулю) и равноускоренного по вертикали. Записав уравнения движения в проекциях на координатные оси Х и Y с учетом начальных условий и подставив координаты точки падения, можно найти время полета и модуль начальной скорости.
имеет вертикальное направление, и его проекция на горизонтальную ось координат равна нулю) и равноускоренного по вертикали. Записав уравнения движения в проекциях на координатные оси Х и Y с учетом начальных условий и подставив координаты точки падения, можно найти время полета и модуль начальной скорости.
Максимальную высоту подъема найдем из условия, что в верхней точке траектории вертикальная составляющая скорости обращается в ноль.
Зная законы изменения проекций скорости на координатные оси со временем, можно найти модуль и направление скорости для любого момента времени. Вектор ускорения постоянен и известен, следовательно, для любого момента времени можно определить нормальное ускорение (т. е. проекцию вектора  на ось n, перпендикулярную вектору скорости и направленную к центру кривизны траектории) и радиус кривизны.
на ось n, перпендикулярную вектору скорости и направленную к центру кривизны траектории) и радиус кривизны.
РЕШЕНИЕ. За начало отсчета примем поверхность Земли под точкой бросания. Ось Х направим горизонтально вдоль поверхности Земли вправо, ось Y – вертикально вверх (рис. 1.1.13). Уравнение движения в проекциях на координатные оси имеет вид:
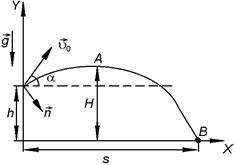 Рис. 1.1.13
Рис. 1.1.13
|
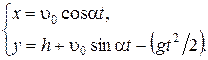 (1.1.16)
(1.1.16)
Скорость тела по оси Y меняется по закону: 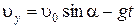 .
.
В момент времени t 1 камень достигает верхней точки своей траектории (точки А, в которой 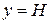 ) и меняет направление Y – составляющей скорости на противоположное (летит вниз). Следовательно,
) и меняет направление Y – составляющей скорости на противоположное (летит вниз). Следовательно, 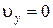 при t = t 1. Отсюда
при t = t 1. Отсюда
 . (1.1.17)
. (1.1.17)
Подставив значение (1.1.17) в уравнение движения (1.1.16), получаем максимальную высоту подъема:
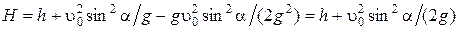 . (1.1.18)
. (1.1.18)
Проверим размерность: 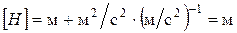 .
.
Найдем начальную скорость  и время полета t. Подставив в уравнение движения (1.16) конечные условия
и время полета t. Подставив в уравнение движения (1.16) конечные условия  ;
;  , получаем:
, получаем:
 ;
; 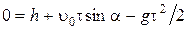 или
или  ;
;
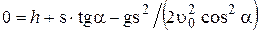 , отсюда
, отсюда 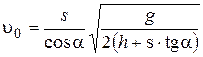 .
.
Проверим размерность: 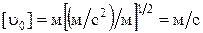 , подставив значение, получим:
, подставив значение, получим:  м/с.
м/с.
Время движения 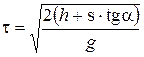 .
.
Проверим размерность: 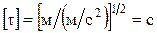 , подставив значение, получим:
, подставив значение, получим: 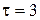 с.
с.
Подставляя значения  и t в выражение (1.1.18), находим Н = 12 м.
и t в выражение (1.1.18), находим Н = 12 м.
 Для определения радиусов кривизны траектории в верхней точке (точка А) и в точке падения (точка В на рис. 1.1.13), найдем в этих точках величину нормального ускорения
Для определения радиусов кривизны траектории в верхней точке (точка А) и в точке падения (точка В на рис. 1.1.13), найдем в этих точках величину нормального ускорения  . Следует напомнить, что полное ускорение в любой точке траектории равно
. Следует напомнить, что полное ускорение в любой точке траектории равно 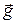 и направлено вертикально вниз.
и направлено вертикально вниз.
Рассмотрим точку А. Скорость 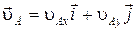 , причем, как было установлено ранее,
, причем, как было установлено ранее, 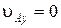 ,
,  , поэтому
, поэтому  – вектор скорости направлен по оси Х, т. е. перпендикулярно к вектору ускорения (рис. 1.1.14). Проекция вектора ускорения на направление скорости равна тангенциальному ускорению и равна нулю:
– вектор скорости направлен по оси Х, т. е. перпендикулярно к вектору ускорения (рис. 1.1.14). Проекция вектора ускорения на направление скорости равна тангенциальному ускорению и равна нулю:  , следовательно,
, следовательно, 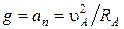 . Отсюда
. Отсюда  . Размерность очевидна. Подставив значение, получим:
. Размерность очевидна. Подставив значение, получим:  м.
м.
 Рис. 1.1.15
Рис. 1.1.15
|
Рассмотрим теперь точку В (рис. 1.1.15). Найдем вектор полной скорости в этой точке. Составляющие вектора 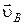 по осям координат равны:
по осям координат равны:
 ;
;  , модуль скорости
, модуль скорости 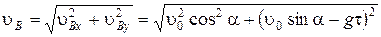 . Вектор скорости
. Вектор скорости 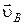 составляет с осью Y угол
составляет с осью Y угол 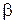 , причем
, причем 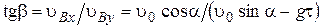 ,
,  .
.
Спроектируем вектор 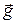 на направление
на направление 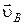 скорости. Нормальное ускорение, как следует из рис.1.1.15, равно
скорости. Нормальное ускорение, как следует из рис.1.1.15, равно 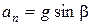 . Радиус кривизны в точке В равен
. Радиус кривизны в точке В равен
 =
=
=  .
.
Проверим размерность:  , подставив значение, получим:
, подставив значение, получим: 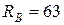 м.
м.
ОТВЕТ: 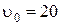 м/с;
м/с; 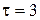 с;
с;  ;
;  м;
м; 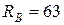 м.
м.
ЗАДАЧА 10. Лифт начал подниматься с постоянным ускорением
 м/с2. Спустя время
м/с2. Спустя время 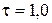 с от потолка кабины лифта отделился и стал падать шуруп. Определить: а) время t падения шурупа до удара о пол кабины; б) путь s, пройденный шурупом за время падения в системе отсчета, связанной с Землей. Высота кабины лифта
с от потолка кабины лифта отделился и стал падать шуруп. Определить: а) время t падения шурупа до удара о пол кабины; б) путь s, пройденный шурупом за время падения в системе отсчета, связанной с Землей. Высота кабины лифта 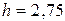 м.
м.
ДАНО:
 м/с2 м/с2
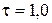 с с
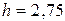 м м
|
| t –? s –? |
АНАЛИЗ. В движении участвуют два тела – шуруп и пол кабины лифта. Движение тел (одномерное, вертикальное) будем рассматривать в системе отчета, связанной с Землей.
Первоначально оба тела перемещались вместе равноускоренно вверх с ускорением  без начальной скорости и в течение времени
без начальной скорости и в течение времени  достигли скорости
достигли скорости 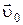 , поднявшись относительно начального положения на некоторую высоту
, поднявшись относительно начального положения на некоторую высоту  . Расстояния между телами при этом оставалось постоянным и равным h.
. Расстояния между телами при этом оставалось постоянным и равным h.
После этого шуруп начал падать свободно, т. е. с ускорением 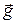 (сопротивление воздуха отсутствует), направленным вертикально вниз. Его скорость в момент начала падения
(сопротивление воздуха отсутствует), направленным вертикально вниз. Его скорость в момент начала падения 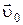 направлена вверх, поэтому шуруп будет двигаться сначала равнозамедленно вверх до тех пор, пока его скорость не станет равной нулю, а затем вниз с тем же ускорением
направлена вверх, поэтому шуруп будет двигаться сначала равнозамедленно вверх до тех пор, пока его скорость не станет равной нулю, а затем вниз с тем же ускорением 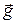 без начальной скорости. Лифт продолжал двигаться вверх с тем же ускорением
без начальной скорости. Лифт продолжал двигаться вверх с тем же ускорением  . Его движение оставалось равноускоренным.
. Его движение оставалось равноускоренным.
За начало отсчета времени в задаче удобно принять момент начала падения шурупа. Начало системы координат следует связать с уровнем пола кабины относительно Земли в начальный момент времени. Записав уравнения движения тел, следует их приравнять и найти время t падения шурупа на пол.
Путь, пройденный шурупом, будет равен сумме высоты его подъема до верхней точки траектории и свободного падения до встречи с полом кабины.
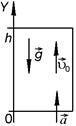 Рис. 1.1.16
Рис. 1.1.16
|
РЕШЕНИЕ. Ось Y направим вертикально вверх (рис.1.1.16). Движение шурупа равнозамедленное с ускорением 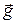 , направленным вниз, и начальной скоростью
, направленным вниз, и начальной скоростью 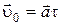 , направленной вверх. Уравнение движения шурупа запишем в виде:
, направленной вверх. Уравнение движения шурупа запишем в виде:
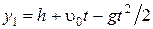 . (1.1.19)
. (1.1.19)
Закон движения пола кабины определяется выражением: 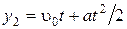 .
.
Условие встречи тел (шуруп упал на пол) имеет вид 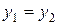 , или
, или  . Отсюда
. Отсюда 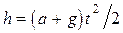 и
и 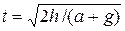 .
.
Проверим размерность:  , подставив значения, получим:
, подставив значения, получим:  c.
c.
Найдем путь, пройденный шурупом относительно Земли. Для этого выясним, на каком этапе движения (при подъеме или при опускании) произошла его встреча с полом. В момент времени  шуруп имел начальную скорость, направленную вверх, которая менялась далее по закону
шуруп имел начальную скорость, направленную вверх, которая менялась далее по закону  , пока не стала равной нулю в момент времени
, пока не стала равной нулю в момент времени  с. Так как
с. Так как 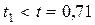 с, очевидно, встреча произошла при опускании шурупа. Согласно уравнению движения (1.1.19) за время t 1шуруп прошел путь
с, очевидно, встреча произошла при опускании шурупа. Согласно уравнению движения (1.1.19) за время t 1шуруп прошел путь
 .
.
Далее в течение времени (t – t 1) шуруп свободно падал до встречи с полом, и пройденный путь составил 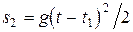 . Полный путь, пройденный шурупом относительно Земли, равен сумме
. Полный путь, пройденный шурупом относительно Земли, равен сумме 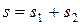 , размерность выражений очевидна, подставив значения, получим:
, размерность выражений очевидна, подставив значения, получим: 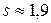 м.
м.
ОТВЕТ: t = 0,71 с; s = 1,9 м.
ЗАДАЧА 11. На высоте 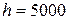 м летит самолет с постоянной скоростью
м летит самолет с постоянной скоростью 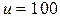 м/с. В момент, когда он находится над зенитной батареей (рис.1.1.17), производится выстрел. Начальная скорость снаряда
м/с. В момент, когда он находится над зенитной батареей (рис.1.1.17), производится выстрел. Начальная скорость снаряда  м/с. Пренебрегая сопротивлением воздуха, найти: а) под каким углом a к горизонту нужно установить ствол орудия, чтобы снаряд и самолет достигли одновременно точки пересечения их траекторий; б) на какую продолжительность полета t нужно установить взрыватель, чтобы снаряд разорвался в точке встречи с целью; в) на какое расстояние
м/с. Пренебрегая сопротивлением воздуха, найти: а) под каким углом a к горизонту нужно установить ствол орудия, чтобы снаряд и самолет достигли одновременно точки пересечения их траекторий; б) на какую продолжительность полета t нужно установить взрыватель, чтобы снаряд разорвался в точке встречи с целью; в) на какое расстояние 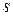 по горизонтали отстоит от батареи точка встречи.
по горизонтали отстоит от батареи точка встречи.
ДАНО:
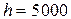 м м
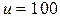 м/с м/с
 м/с м/с
|
a –? t –?  –? –?
|
АНАЛИЗ. Эта задача на кинематику движения двух тел. В движении участвуют: самолет, находящийся на высоте h над Землей и движущийся равномерно по горизонтали со скоростью u; и снаряд, выпущенный под углом 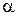 к горизонту.
к горизонту.
 Из условия задачи следует, что в момент выстрела самолет находился над пушкой, т. е. оба тела находились на одной вертикальной прямой. Поэтому целесообразным является принять за начало отсчета пушку, систему отсчета связать с Землей, ось Y направить вертикально вверх, ось X – горизонтально по движению самолета. За начало отсчета времени удобно принять момент выстрела.
Из условия задачи следует, что в момент выстрела самолет находился над пушкой, т. е. оба тела находились на одной вертикальной прямой. Поэтому целесообразным является принять за начало отсчета пушку, систему отсчета связать с Землей, ось Y направить вертикально вверх, ось X – горизонтально по движению самолета. За начало отсчета времени удобно принять момент выстрела.
Направление скорости снаряда 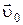 задано углом
задано углом 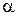 , который нужно определить. Сопротивление воздуха отсутствует (по условию), поэтому ускорение снаряда постоянно и равно
, который нужно определить. Сопротивление воздуха отсутствует (по условию), поэтому ускорение снаряда постоянно и равно 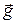 . Векторы скорости и ускорения в начальный момент времени образуют угол, отличный от нуля и
. Векторы скорости и ускорения в начальный момент времени образуют угол, отличный от нуля и 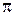 , поэтому траекторией движения является плоская кривая. Это плоское движение можно представить, как отмечалось ранее, суммой двух прямолинейных движений – равномерного со скоростью
, поэтому траекторией движения является плоская кривая. Это плоское движение можно представить, как отмечалось ранее, суммой двух прямолинейных движений – равномерного со скоростью 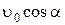 по оси X, и равнопеременного по оси Y (составляющая начальной скорости снаряда
по оси X, и равнопеременного по оси Y (составляющая начальной скорости снаряда 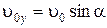 направлена по оси Y, а ускорение
направлена по оси Y, а ускорение 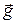 – против оси).
– против оси).
Записав уравнение движения тел в проекциях на координатные оси, и приравняв соответствующие уравнения, получим два уравнения, в которых неизвестны угол 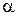 и время полета t. Это время, на которое следует установить взрыватель. Зная время полета и подставив его в любое из уравнений движения по оси X, найдем расстояние s от батареи до места взрыва.
и время полета t. Это время, на которое следует установить взрыватель. Зная время полета и подставив его в любое из уравнений движения по оси X, найдем расстояние s от батареи до места взрыва.
РЕШЕНИЕ. Уравнение движения самолета в координатах x, y имеет вид
 . (1.1.20)
. (1.1.20)
Снаряд движется со скоростью, направленной под углом 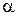 к горизонту и ускорением
к горизонту и ускорением 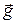 , направленным вертикально вниз. Его уравнение движения запишем в виде:
, направленным вертикально вниз. Его уравнение движения запишем в виде:
 ;
; 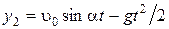 . (1.1.21)
. (1.1.21)
В момент встречи тел должны выполняться условия: 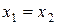 ;
;  , подставив в которые выражения (1.1.20) и (1.1.21), получаем:
, подставив в которые выражения (1.1.20) и (1.1.21), получаем:  ;
;  . Отсюда находим угол
. Отсюда находим угол  ;
;  °, и продолжительность полета, решив квадратное уравнение относительно t:
°, и продолжительность полета, решив квадратное уравнение относительно t:
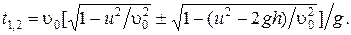
Если бы не произошло взрыва, снаряд и самолет встретились бы дважды – при движении снаряда вверх (в момент времени t 1) и при возвращении вниз (в момент времени t 2). Но так как взрыв имеет место, то необходимо взять только меньшее значение t. Это соответствует ситуации, когда снаряд движется вверх и встречается с самолетом. Поэтому
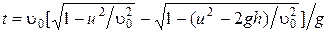 .
.
Проверим размерность: 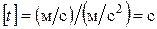 . Подставив значения, получим: t = 11,5 c.
. Подставив значения, получим: t = 11,5 c.
Расстояние, на которое отстоит от батареи точка встречи, найдем, подставив значение t в первое уравнение системы (1.1.20). Получаем 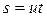 . Правильность формулы по размерности очевидна, подставив значения, получим:
. Правильность формулы по размерности очевидна, подставив значения, получим:  м.
м.
ОТВЕТ:  °; t =11,5 c;
°; t =11,5 c;  м.
м.
ЗАДАЧА 12. Твердое тело начинает вращаться вокруг неподвижной оси с угловым ускорением  , где
, где  рад/с3. Через сколько времени после начала вращения вектор полного ускорения произвольной точки тела будет составлять угол
рад/с3. Через сколько времени после начала вращения вектор полного ускорения произвольной точки тела будет составлять угол 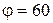 ° с ее вектором скорости?
° с ее вектором скорости?
ДАНО:
 рад/с2 рад/с2
 рад/с3 рад/с3
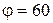 ° °
|
| t –? |
АНАЛИЗ. Эта задача на кинематику вращательного движения. Твердое тело совершает ускоренное вращение без начальной угловой скорости. При вращении твердого тела вокруг неподвижной оси все его точки имеют одинаковые угловые ускорения, поэтому целесообразно рассмотреть произвольную материальную точку, которая совершает вращение по окружности радиуса, равному ее удалению от оси.
 Рис. 1.1.18
Рис. 1.1.18
|
Так как движение ускоренное 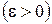 , то вектор тангенциального ускорения точки
, то вектор тангенциального ускорения точки  совпадает по направлению с вектором ее скорости, и для определения угла между векторами полного ускорения
совпадает по направлению с вектором ее скорости, и для определения угла между векторами полного ускорения  и скорости достаточно определить угол между векторами
и скорости достаточно определить угол между векторами  и
и  . По условию задачи этот угол известен, и выразив его через
. По условию задачи этот угол известен, и выразив его через  и
и  , которые зависят от времени, мы найдем искомое время.
, которые зависят от времени, мы найдем искомое время.
РЕШЕНИЕ. Из рис. 1.1.18 видно,
что 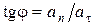 , (1.1.22)
, (1.1.22)
где 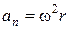 – модуль нормального ускорения.
– модуль нормального ускорения.
Модуль тангенциального ускорения: 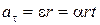 . (1.1.23)
. (1.1.23)
Угловая скорость w связана с угловым ускорением соотношением: 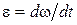 ,
,
поэтому  , где С – произвольная постоянная
, где С – произвольная постоянная
В момент времени  угловая скорость
угловая скорость 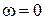 , поэтому
, поэтому  . Окончательно имеем:
. Окончательно имеем:
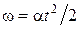 ;
;  . (1.1.24)
. (1.1.24)
Подставив выражения для ускорений из (1.1.24) и (1.1.23) в формулу (1.1.22),
получаем: 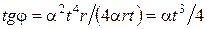 .
.
По условию задачи 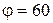 °, тогда
°, тогда 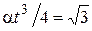 , и
, и 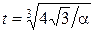 . Правильность формулы по размерности очевидна. Подставив значения
. Правильность формулы по размерности очевидна. Подставив значения 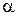 , найдем
, найдем 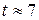 с.
с.
ОТВЕТ: 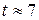 с.
с.
ЗАДАЧА 13. Обруч радиусом R катится по горизонтальной поверхности. Скорость центра обруча постоянна и равна 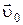 (рис. 1.1.19). Определить: а) модуль и направление угловой скорости
(рис. 1.1.19). Определить: а) модуль и направление угловой скорости 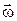 обруча; б) скорости
обруча; б) скорости 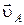 и
и 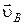 точек А и В; в) модули и направления ускорений
точек А и В; в) модули и направления ускорений  ;
;  ;
;  и скоростей
и скоростей 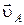 ;
; 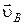 ;
; 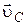 точек А, В, С в системе отсчета, в которой центр обруча покоится; г) ускорения точек А, В, С в системе отсчета, связанной с поверхностью; д) радиус
точек А, В, С в системе отсчета, в которой центр обруча покоится; г) ускорения точек А, В, С в системе отсчета, связанной с поверхностью; д) радиус 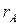 кривизны траектории в точке А.
кривизны траектории в точке А.
ДАНО:
R
|
а) 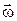 –?
б) –?
б) 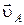 –? –?
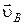 –?
в) –?
в)  ; ;  ; ; 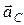 –? –?
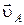 ; ; 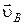 ; ; 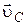 –?
г) –?
г)  ; ;  ; ; 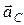 –?
д) –?
д) 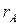 –? –?
|
АНАЛИЗ. Обруч участвует в двух движениях – поступательном со скоростью центра масс и вращательном с угловой скоростью 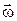 относительно центра масс. Используя связь угловых и линейных характеристик движения и теорему сложения скоростей для разных точек обруча, находим скорости и ускорения этих точек.
относительно центра масс. Используя связь угловых и линейных характеристик движения и теорему сложения скоростей для разных точек обруча, находим скорости и ускорения этих точек.
РЕШЕНИЕ. а) Центр масс О обруча движется вправо, поэтому вращение точек обруча относительно точки О происходит по часовой стрелке. Следовательно, вектор угловой скорости 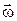 направлен перпендикулярно плоскости чертежа за чертеж. Модуль угловой скорости равен
направлен перпендикулярно плоскости чертежа за чертеж. Модуль угловой скорости равен
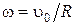 . (1.1.25)
. (1.1.25)
б) Найдем скорости точек А и В. Точка А участвует одновременно в двух движениях: поступательном со скоростью 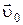 и вращательном относительно точки О с угловой скоростью
и вращательном относительно точки О с угловой скоростью  . Скорость
. Скорость  точки А во вращательном движении (рис.1.1.20) направлена по касательной к обручу вправо и равна
точки А во вращательном движении (рис.1.1.20) направлена по касательной к обручу вправо и равна  , где
, где 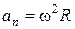 – нормальное ускорение. Подставив значение
– нормальное ускорение. Подставив значение  из (1.1.25), получаем:
из (1.1.25), получаем:  .
.
Таким образом, полная скорость точки А равна 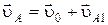
или в скалярной форме  . (1.1.
. (1.1.
Date: 2015-09-03; view: 7186; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |